Modeling Oil/Water Emulsion Separation in Batch Systems

Introduction

Separating liquid-liquid dispersions is a widespread issue in industries like petroleum, petrochemical, hydrometallurgy, nuclear fuel processing, and chemicals [1, 2]. This separation is typically done using gravity settlers and centrifuges, designed from expensive pilot plant tests. Researchers have tried to grasp this process by observing droplet sedimentation, creaming, and coalescence in small-scale, cost-effective batch separators. Predicting the system parameters like residence time and maximum droplet size in liquid-liquid phase separation is crucial for the efficient design and operation of real-size decanters [3]. Accurate predictions of residence time ensure that the mixture has sufficient time to separate into distinct phases, optimizing the separation process. An underestimation can lead to incomplete separation, affecting product quality and efficiency, while an overestimation may result in oversized equipment or increased energy consumption [4]. Due to the complexity of physical experiments, employing mathematical models and simulations is becoming a preferred approach to study and design batch settlers.

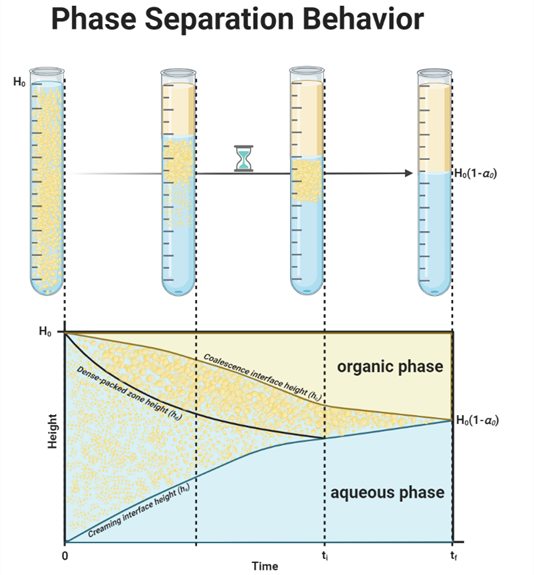
Figure 1 illustrates a typical batch gravity settler operation, identifying four key areas during phase separation: an aqueous phase, an organic phase, a dense-packed zone, and a creaming/sedimentation zone. At the start (time t = 0), either sedimentation or creaming occurs, depending on the density of the dispersed phase relative to the continuous phase. Depending on the emulsion type (water in oil or oil in water), either sedimentation or creaming occurs. These two mechanisms in liquid-liquid decantation can happen simultaneously, but often one is more dominant, influenced by the densities of the liquids [4]. Sedimentation is a process that occurs when the dispersed phase has a higher density than the continuous phase, and due to gravity, droplets move downward in the continuous phase. Creaming is also a gravity-driven process, and it involves the upward migration of droplets in the dispersion layer because the dispersed phase is lighter than the continuous phase. In Figure 1 the light phase is dispersed, therefore this work will use the term ‘creaming’ for clarity. Initially, droplets grow through droplet-droplet coalescence in the dispersion zone. If this growth is faster than droplet–interface coalescence (droplets merging with their homophase), they accumulate in the dense-packed zone and later merge with their homophase [5]. Therefore, the droplets at the interface end up larger than those originally formed. At a so-called inflection point (t = t_i), where h_d equals h_s, the creaming process concludes, resulting in three distinct layers: the aqueous phase, the organic phase, and the dense-packed zone. Eventually, after a certain period (t = t_f), all droplets vanish, leaving a distinct interface [6].

Many authors have introduced sedimentation-based models to understand the mechanism of phase separation in emulsions [6-12]. Stokes (1851) was the first to analyze sedimentation in significant depth, which led to a formulation of the equation for the settling velocity of a single hard sphere, known as Stoke’s law [13]. Nadiv and Semiat (1995) conducted experimental research to examine the influence of mixing conditions and dispersion height on the separation of batch dispersions using two different settler diameters [14]. However, they did not deliberately alter the dispersion holdup. Their model for sedimentation was built upon the analysis by Aris and Amundson (1973) concerning batch precipitation of solid suspensions [15]. To describe the coalescence profile, an empirical formula was employed. Their model incorporated four adjustable parameters that must be identified through experimental sedimentation and coalescence profiles. Jeelani and Hartland have adapted the Stokes law and the incorporation of the physical and chemical properties of droplets into sedimentation [7]. The model suggested by Jeelani and Hartland requires prior knowledge of the interfacial coalescence timeframe and initial droplet size [16]. In addition, they provide a formula for determining the initial droplet diameter based on the initial sedimentation velocity. As Noïk et al. (2013) reported, coalescence happens when two droplets approach and collide (droplet-droplet coalescence) or when a droplet collides into its homophase [17]. In their study, a model, including this coalescence behavior, is developed to predict the settling time of batch separators. However, it is essential to note that the model does not directly account for the effect of additives like surfactant concentration on sedimentation and coalescence behavior. It should be highlighted that their model utilized a collision efficiency coefficient, as the primary empirical parameter. This parameter is predominantly influenced by the physicochemical characteristics of the water-oil interfacial film, with factors such as oil composition and the presence of additives like demulsifiers playing significant roles.

Model Development

Droplet-droplet and droplet-interface coalescence rates are functions of various factors, including the initial droplet siz, inlet dispersed phase volume fraction, and the physical properties of the liquids, such as densities, viscosities, and interfacial tension. Equipment geometry, such as the settling area and equipment internals, also comes into play. Hence, understanding these parameters’ role on phase separation rate is critical. Droplet-droplet coalescence and droplet-interface coalescence are depicted in Figure 2.

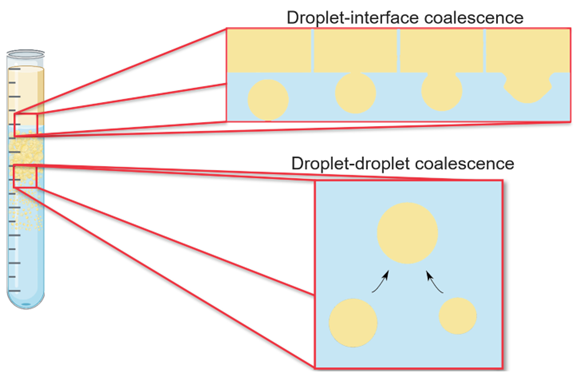
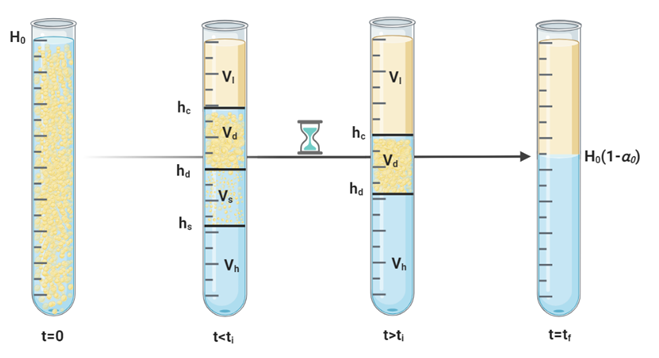
Figure 3 depicts the decantation process in a separation vessel, showing four layers initially: an aqueous phase, an organic phase, a dense-packed zone, and a creaming zone. The process is split into two stages: before and after the inflection point (t_i). Prior to t_i, the creaming zone’s height (h_s), the dense-packed zone’s height (h_d), and the coalescence interface height (h_c) define the boundaries of the layers. After t_i, the system stabilizes to just the dense-packed zone and distinct aqueous and organic phases. The changes in these interfaces over time are critical for understanding the separation process, which will be further explained. The next sections will detail the formulas for these stages and explore the driving mechanisms behind the interface movements and the physical processes they entail.

Based on the overall volume in a vessel as depicted in Figure 1, the volume balance can be represented mathematically. The total volume, V_t​, is the sum of the oil volume, V_o, ​ and the water volume, V_w:

Given that V_o = V_tα₀, where α₀​ is the initial volume fraction of dispersed phase, we can derive the following expression for V_w:

Moreover, based on Figure 3, the total volume before t_i can be broken down into the volumes of the clear light phase at the top (V_l), dense packed layer (V_d), the creaming zone (V_s), and the clear heavy phase at the bottom (V_h),:

The volume of oil, V_o, can be expressed as:

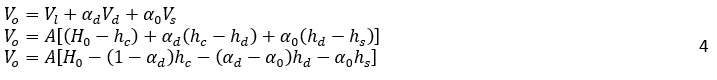
Where H₀, is the vessel height, A is the vessel cross-sectional, and α_d is the volume fraction of dispersed phase in dense-packed zone. In the dense-packed zone, dispersed phase droplets become more compact as they get closer together. Theoretically, the packing of hard spheres can reach a maximum value of 0.74. However, some literature reports a lower maximum packing density, around 0.65, for certain systems or under specific conditions due to droplet deformation [6, 16]. Similarly, for the water volume, V_w:

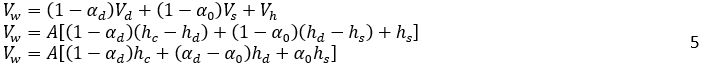
By inserting equations 4 and 5 into equation 2, and considering that the vessel’s cross-sectional area, A, is constant, we arrive at:

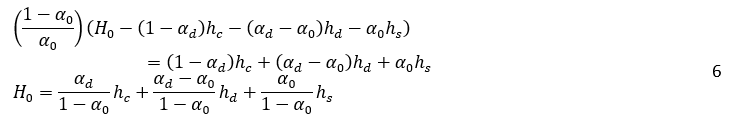
By taking the time derivative of equation 6, the relation between the height of creaming zone (h_s), the dense-packed zone (h_d), and coalescence interface (h_c) before t_i can be determined by using the following expression:

Likewise, after t_i, the overall volume is made up of the clear light phase on top (V_l), the clear water phase at the bottom (V_h), and the dense-packed zone (V_d).

After t_i there is no creaming zone, and in the dense-packed zone the dispersed phase volume fraction is (α_d) higher than the initial volume fraction (α₀) due to droplets compaction. then the volume of oil, V_o, can be expressed as:

Similarly, for the water volume, V_w:

When equations 9 and 10 are substituted into equation 2 and it is taken into account that the cross-sectional area of the vessel, A, remains constant, the following result is derived:

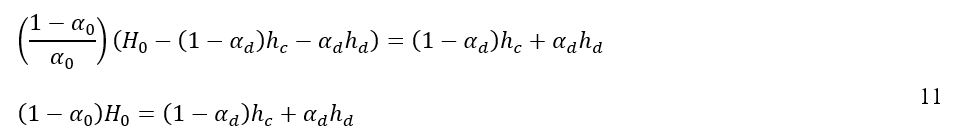
By taking the time derivative of equation 11, the relation of coalescence interface and dense-packed zone height for the system can be determined by using the following expression:

Established methods exist to determine the size of gravity separators to enhance phase separation. Typically, the separator’s dimensions are calculated based on the settling (or ascending) time of droplets following the principles of sedimentation for spherical particles in a Newtonian fluids at low Reynolds numbers. As Noïk et al. (2013) proposed, creaming velocity can be determined by considering initial factors like volume fraction, droplet diameter and physical properties of system [17]:

The term D² accounts for the impact of droplet size increase, as a result of coalescence, on their movement within the system, (1-α₀)^nRZ is a hindered settling factor and takes account of the influence of the droplet concentration in the dispersed phase on the creaming rate. The value of n_RZ, which falls between 2.3 and 5.5, is known as the Richardson-Zaki coefficient [27]. Snabre and Mills developed a comprehensive physical framework and expanded on the Richardson-Zaki formula. They introduced a variable exponent “n” influenced by the Reynolds number. In scenarios with a low Reynolds number, “ n_RZ ” approximates 5.5, whereas in denser systems, they recommend an exponent of 5.1 [28]. In this study n_RZ=5.3 is adopted as used in several earlier studies [9, 10, 16]. D represents the droplet diameter at time (t), while D₀ represents the initial average droplet diameter. U_t is the terminal velocity and is evaluated with Stokes law as:

Δρ is density difference between the dispersed and continuous phases, g is acceleration due to gravity and µ_c is dynamic viscosity of continuous phase.

The volume rate of interfacial coalescence per unit area is given by [20]:

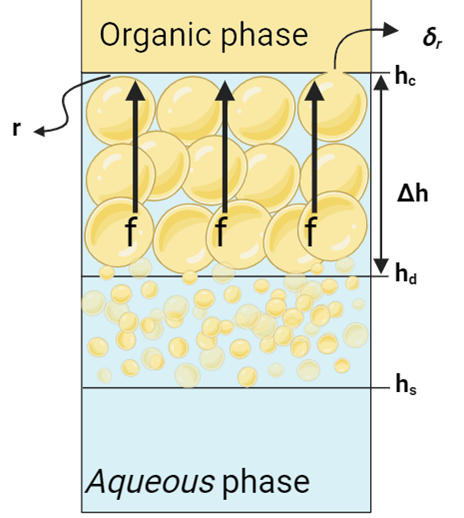
in which τ represents the time it takes for droplets with diameter D to coalesce with the interface. Following Jeelani and Hartland’s (1998) work, τ is inversely related to the force on the film draining over the droplet [16]. In dense-packed layer, as the Figure 4 shows, this force relates to the height difference Δh = h_c ─ h_d, and for a single layer of droplets at the interface, it’s related to their diameter D. The droplet-interface coalescence time is then given by:

where τ₀ is the time needed for droplets of diameter D₀ in a monolayer to coalesce with the interface. τ₀ can be calculated using Jeelani and Hartland’s (1994) equation [21]:

In Figure 4 and Equation 16, f is the force on the draining film of the continuous phase with radius r, while δ_r represents the film’s thickness at the point of rupture. In other words, δ_r is the critical thickness at which the film breaks or ruptures. When the film radius reaches the critical thickness, it becomes unstable and ruptures. The surface mobility, m, combines the mobilities from induced circulation in nearby phases and the gradient of interfacial tension. In cases where the surface is immobile, as assumed in this work, m is set to zero.

For a drop of diameter D₀:

For small droplets, the radius of the film r at an interface is equivalent to the radius of an individual droplet. The critical thickness of the film at the point of rupture, δ_r, can be determined using Vrij and Overbeek’s (1968) equation[22]:

where σ is the interfacial tension and A_m is the Hamaker constant. The Hamaker coefficient can usually be measured experimentally, although its values for a specific system in the literature may differ by a factor of 10. However, for numerous systems, the Hamaker coefficient typically falls within the same order of magnitude [23]. The radius of the draining film, r, can be calculated using the modified Derjaguin and Kussakov’s (1939) equation for a droplet at a deformable interface [16, 24]:

In the above equations, the evolution of droplet size due to droplet-droplet coalescence remains undefined. For the calculation of D, following formula suggested by Noïk et al. (2013) [17]:

θ is an empirical collision efficiency parameter which includes physicochemical characteristics of the interfacial film (elasticity) and some hydrodynamic aspect of droplet approach and collision (film drainage).

Results and discussion

The model is tested using an experimental dataset, focusing on liquid-liquid phase separation [14, 16]. Key parameters included the type of separation (oil in water), initial test tube height (H₀), initial droplet diameter (D₀), phase viscosities (µ) and densities (ρ), interfacial surface tension (σ), and initial dispersed phase volume fraction (α₀). Additionally, data on coalescence and creaming heights versus time were key for model validation. The first experimental dataset from Jeelani and Hartland (1998) is summarized in Table 1 and Figure 5 (a) [16].

Table 1 – Summary of the first set of experimental data, including Initial height of emulsion, Initial droplet diameter, Initial volume fraction of the dispersed phase. These experimental data were derived from Jelaani and Hartland (1998)a [16].
Parameter/Experiment	I	II	III	IV	V	VI
H0	0.457	0.686	0.915	0.915	0.915	0.915
D0	847×10-6	847×10-6	847×10-6	847×10-6	680×10-6	710×10-6
α0	0.3	0.3	0.3	0.4	0.5	0.6
a 25% decane in paraffin oil mixture (density: 837.3 kg/m³, viscosity: 1.26×10-3 Pas at 20 °C) dispersed in demineralized water (density: 996 kg/m³, viscosity: 1×10-3 Pas) obtained using 25 mm diameter settler. The interfacial tension was 52.4 ×10-3 N/m. The value of αd=0.65.

In the droplet coalescence model formulation, oil droplets are assumed uniformly dispersed in the water phase and initially follow a normal distribution with a specified mean diameter and standard deviation. The mentioned experimental campaign did not include measuring the initial droplet population. As an educated guess, the initial population was assumed normal distribution and characterized by a 10% standard deviation. This is based on the experimental study of Boxall et al. (2010) and is in accordance with the results presented in Noïk et al. (2013) [17, 25]. The estimated value of the Hamaker constant, A_m=8.15 ×10^-21, aligns within the same order of magnitude as values documented in related literature within the field [10, 16].  Once this initial distribution is formed, the population of droplets will then depend on the dispersion volume.

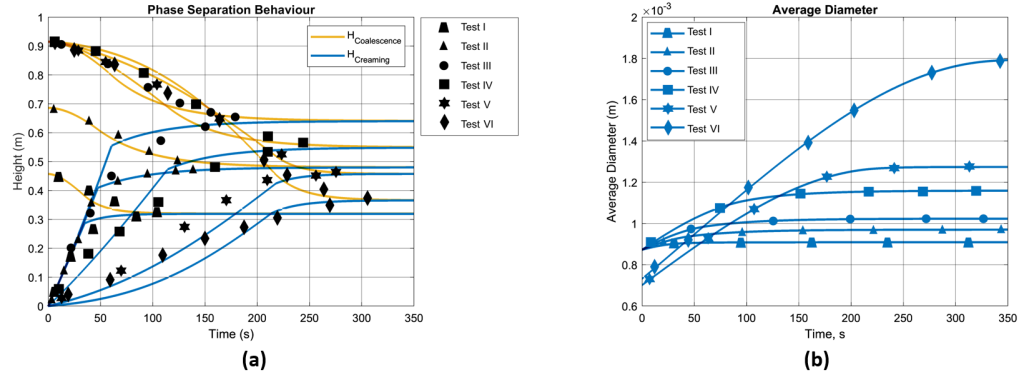
The Figure 5 (a) presents phase separation over time, comparing the experimental results with numerical predictions. The graph shows trends in coalescence and creaming heights, marked by black dots for experimental values and continuous lines for predictions across experiment I to VI. In line with Henschke’s research [6], creaming height’s trend, remains largely unchanged despite different phase ratios, suggesting minimal influence from this variable. Also, observation in coalescence height across numerical results is consistent with Jeelani and Hartland’s report, noting distinct coalescence rates against constant creaming due to varying parameters. The Figure 5 (b) shows the percentage of the dispersion fraction over time. In Tests I and II, the emulsion separates faster at first, indicated by steep initial drops. The quick separation in these tests is due to lower initial volume of the emulsion. Moving from Tests I to III, the decline is less sharp, meaning the separation starts more slowly. This slower start is linked to larger initial volumes in Tests III and VI, which show a gradual separation at the beginning. The lower rate of leveling off after inflection point, is influenced by the starting size of the droplets and the height of the mixture. Across all tests, the pattern remains consistent: an initial rapid decrease due to creaming, followed by a gradual slowdown as the separation depends on droplet-droplet and droplet-interface coalescence. The Figure 5 (c) shows how the predicted average size of droplets increases as time passes in six tests. Although Tests I to IV share the same starting size for droplets, their differing initial conditions lead to varied final sizes. This suggests that the height and concentration of the emulsion initially can influence how much droplets grow. For Tests V and VI, which start with smaller droplets, the rate of growth and the size they reach by the end differ, indicating that the initial volume fraction has a significant impact on the coalescence process and how droplets merge over time.

Conclusion

As we wrap up our exploration into the world of oil and water separation, it’s clear that the model we’ve discussed is not just a set of equations and theories. It’s a bridge connecting the complex dance of liquid-liquid phase separation with practical, real-world applications. By standing up to the rigors of experimental validation, this model has proven itself as a reliable navigator through the intricate dynamics of separating two substances that nature intended to keep apart.

So, as we conclude, let’s not view this model merely as a collection of mathematical expressions, but as a testament to human ingenuity’s role in solving the puzzles presented by nature. The road ahead is promising, illuminated by the insights gained from this model, guiding us towards a future where the separation of oil and water is not just necessary, but a process refined to near perfection.🔬💧🌍

References

1.            Ahmad, J. and L.M. Nollet, Nanoemulsions in Food Technology: Development, Characterization, and Applications. 2021: CRC Press.

2.            Hidayah, N.N. and S.Z. Abidin, The evolution of mineral processing in extraction of rare earth elements using liquid-liquid extraction: A review. Minerals Engineering, 2018. 121: p. 146-157.

3.            Stewart, M. and K. Arnold, Gas-liquid and Liquid-liquid Separators. 2008: Gulf Professional Publishing.

4.            Hooper, W. and L. Jacobs Jr, Decantation. Handbook of Separation Methods for Chemical Engineers (PA Schweitzer, ed.), McGraw-Hill, New York, 1979: p. 1.343-1.358.

5.            Thaker, A.H. and V.V. Buwa, Experimental investigations of interfacial and binary coalescence of multilayered drops. Industrial & Engineering Chemistry Research, 2019. 58(18): p. 7620-7632.

6.            Henschke, M., L.H. Schlieper, and A. Pfennig, Determination of a coalescence parameter from batch-settling experiments. Chemical Engineering Journal, 2002. 85(2-3): p. 369-378.

7.            Jeelani, S.A.K. and S. Hartland, Prediction of dispersion height in liquid-liquid gravity settlers from batch settling data. Chemical engineering research & design, 1986. 64(6): p. 450-460.

8.            Bhardwaj, A. and S. Hartland, Kinetics of coalescence of water droplets in water-in-crude oil emulsions. journal of dispersion science andtechnology, 1994. 15(2): p. 133-146.

9.            Jeelani, S., K. Panoussopoulos, and S. Hartland, Effect of Turbulence on the Separation of Liquid− Liquid Dispersions in Batch Settlers of Different Geometries. Industrial & engineering chemistry research, 1999. 38(2): p. 493-501.

10.          Aleem, W., et al., Experimental investigation and mathematical modeling of oil/water emulsion separation effectiveness containing alkali-surfactant-polymer. Journal of Dispersion Science and Technology, 2021. 42(9): p. 1286-1298.

11.          Khan, J.A., et al., Influence of alkali-surfactant-polymer flooding on the coalescence and sedimentation of oil/water emulsion in gravity separation. Journal of Petroleum Science and Engineering, 2019. 173: p. 640-649.

12.          Grimes, B., Population balance model for batch gravity separation of crude oil and water emulsions. Part I: model formulation. Journal of Dispersion Science and Technology, 2012. 33(4): p. 578-590.

13.          Stokes, G.G., On the effect of the internal friction of fluids on the motion of pendulums. 1851.

14.          Nadiv, C. and R. Semiat, Batch settling of liquid-liquid dispersion. Industrial & engineering chemistry research, 1995. 34(7): p. 2427-2435.

15.          Schneider, D.R., R. Aris, and N.R. Amundson, An analysis of chemical reactor stability and sensitivity—XIV the effect of the steady state hypothesis. Chemical Engineering Science, 1973. 28(3): p. 885-896.

16.          Jeelani, S.A.K. and S. Hartland, Effect of dispersion properties on the separation of batch liquid− liquid dispersions. Industrial & engineering chemistry research, 1998. 37(2): p. 547-554.

17.          Noïk, C., T. Palermo, and C. Dalmazzone, Modeling of liquid/liquid phase separation: Application to petroleum emulsions. Journal of Dispersion Science and Technology, 2013. 34(8): p. 1029-1042.

18.          Richardson, J.T., Sedimentation and fluidization: Part I. Trans. Inst. Chem. Engrs., 1954. 32: p. 35-52.

19.          Snabre, P. and P. Mills, Settling and fluidization of non Brownian hard spheres in a viscous liquid. The European Physical Journal E, 2000. 1: p. 105-114.

20.          Vohra, D. and S. Hartland, Shape of a vertical column of drops approaching an interface. AIChE Journal, 1978. 24(5): p. 811-817.

21.          Jeelani, S. and S. Hartland, Effect of interfacial mobility on thin film drainage. Journal of colloid and interface science, 1994. 164(2): p. 296-308.

22.          Vrij, A. and J.T.G. Overbeek, Rupture of thin liquid films due to spontaneous fluctuations in thickness. Journal of the American Chemical Society, 1968. 90(12): p. 3074-3078.

23.          Visser, J., On Hamaker constants: A comparison between Hamaker constants and Lifshitz-van der Waals constants. Advances in colloid and interface science, 1972. 3(4): p. 331-363.

24.          Derjaguin, B. and M. Kussakov, Anomalous properties of thin polymolecular films. Acta Physicochim. URSS, 1939. 10(1): p. 25-44.

25.          Boxall, J.A., et al., Measurement and calibration of droplet size distributions in water-in-oil emulsions by particle video microscope and a focused beam reflectance method. Industrial & engineering chemistry research, 2010. 49(3): p. 1412-1418.